Using SPSS and R to Calculate Ordinal Alpha and Omega Internal Consistency

Using SPSS and R to Calculate Ordinal Alpha and Omega Internal Consistency

(If you'd like to see how I created the SPSS Custom Dialog, comment below)

2024 Update: JAMOVI now offers Ordinal Alpha, and it is way easier to use than SPSS.

Jamovi is free and powerful: jamovi.org

Internal consistency estimates for Likert-type data can be artificially attenuated if we assume interval level data (Gaderman et al., 2012). And, the alpha based on Cronbach's 1951 paper suffers from some limitations as an indicator of internal consistency (Dunn et al., 2014). Thus, Omega has been proposed as an alternative to alpha.

Here I highlight the use of  the R-package 'userfriendlyscience' (Peters, 2014) for calculating ordinal Omega and alpha, and I will include a very simple SPSS extension package for those less comfortable with R. The package allows you to easily point and click for fast calculations of Omega.

Note: For SPSS Ver 24, you need R 3.2.x, not the new R (which is 3.4.0).


To use the extension you need to:
1. install R from here https://www.r-project.org/
2. install the 'userfriendlyscience' package in R (see note at bottom about installing an older version for R 3.2.x)
3. install Essentials for R from SPSS. Download and install for your version of SPSS. You may need to set-up an SPSS support account.
4. download and then install my custom dialog extension (this is shared in my google drive. click and follow link, then download)

Let me now if you have problems. I am tweaking the interface to make it more fancy. But I want the simple interface to remain an option.



Calculating Omega and Alpha involves using the scaleReliability command in R.

e.g.,

> scaleReliability(dat = TrimAllSurveysForR, items = c('PRFQ2','PRFQ5','PRFQ8','PRFQ14','PRFQ17'))


gives the following output:

---------------------------------------------------------------
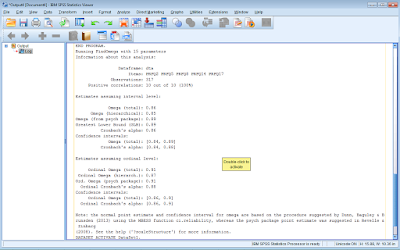
Running FindOmega with 15 parameters
Information about this analysis:

                 Dataframe: dta
                     Items: PRFQ2 PRFQ5 PRFQ8 PRFQ14 PRFQ17
              Observations: 317
     Positive correlations: 10 out of 10 (100%)

Estimates assuming interval level:

             Omega (total): 0.86
      Omega (hierarchical): 0.85
Omega (from psych package): 0.89
Greatest Lower Bound (GLB): 0.89
          Cronbach's alpha: 0.86
Confidence intervals:
             Omega (total): [0.84, 0.89]
          Cronbach's alpha: [0.84, 0.88]

Estimates assuming ordinal level:

     Ordinal Omega (total): 0.91
 Ordinal Omega (hierarch.): 0.87
Ord. Omega (psych package): 0.91
  Ordinal Cronbach's alpha: 0.88
Confidence intervals:
     Ordinal Omega (total): [0.86, 0.9]
  Ordinal Cronbach's alpha: [0.86, 0.9]

Note: the normal point estimate and confidence interval for omega are based on the procedure suggested by Dunn, Baguley & Brunsden (2013) using the MBESS function ci.reliability, whereas the psych package point estimate was suggested in Revelle & Zinbarg
(2008). See the help ('?scaleStructure') for more information.

-------------------------------------------------------------

So, the package actually includes loads of useful information, including citations.


To install and use the SPSS extension in Step 4 above:

1.Select the Install Custom Dialog Option



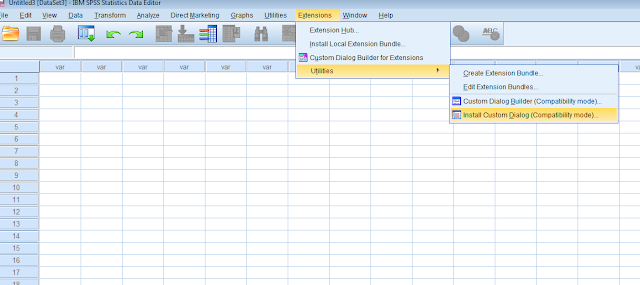
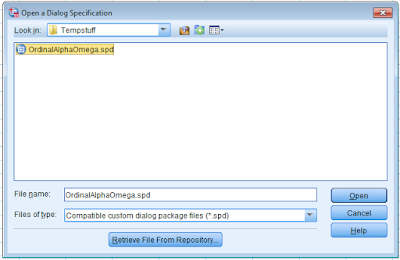
2. Open the OrdinalAlphaOmega.spd file from the folder where you saved it.


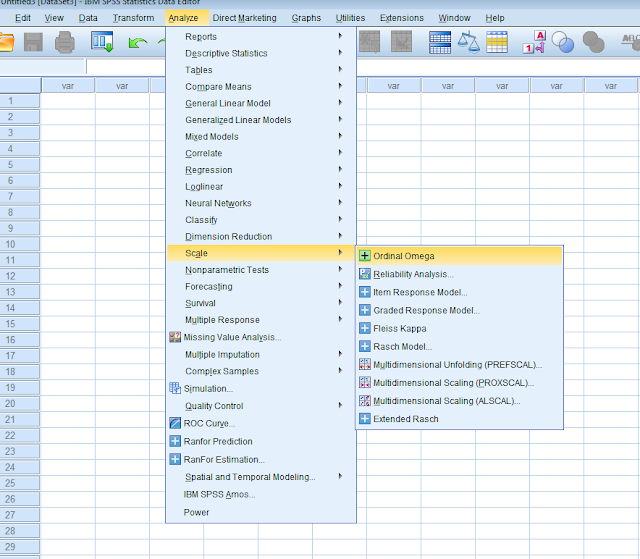
3. Click OK to install, and the command should now appear in the Analyze, Scale drop-down menu.



You can now use the Ordinal Omega command and it opens up the dialog box like this.



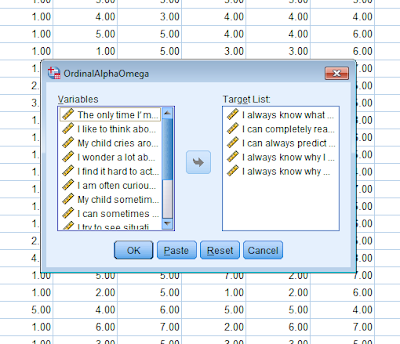
Select ok, and the standard SPSS output is produces, but it includes the same R output as above.




Keywords: SPSS, userfriendlyscience, Omega, reliability, Cronbach


References

Dunn, T. J., Baguley, T., & Brunsden, V. (2014). From alpha to omega: A practical solution to the pervasive problem of internal consistency estimation. British Journal of Psychology, 105(3), 399–412. https://doi.org/10.1111/bjop.12046

Gadermann, A. M., Guhn, M., & Zumbo, B. D. (2012). Estimating Ordinal Reliability for Likert-Type and Ordinal Item Response Data: A Conceptual, Empirical, and Practical Guide. Practical Assessment, Research & Evaluation, 17(3).

Peters, G.-J. Y. (2014). The alpha and the omega of scale reliability and validity: Why and how to abandon Cronbach’s alpha and the route towards more comprehensive assessment of scale quality. European Health Psychologist, 16(2), 56–69.

---------------------------------------------------------------------------------------------------------------------
NOTE: To install an older version of userfriendlyscience, first install 'devtools' and use the following code in R:

require(devtools)
install_version("userfriendlyscience", version = "0.4-1", repos = "http://cran.us.r-project.org")

This loads an older version of 'userfriendlyscience' that is compatible with R3.2.5 and SPSS24....and in 2 months I will be using SPSS 25....sheesh.

---------------------------------------------------------------------------------------------------------------------

EDIT: I have attached the R Markdown here, in case this is useful for you:


<!-- Styles for R syntax highlighter

scaleReliability(dat = Dataset, items = c('prfq2','prfq5','prfq8','prfq14',
  'prfq17'))

## 10 cells were adjusted for 0 values using the correction for continuity. Examine your data carefully.

## 
## Information about this analysis:
## 
##                  Dataframe: Dataset
##                      Items: prfq2, prfq5, prfq8, prfq14, prfq17
##               Observations: 317
##      Positive correlations: 10 out of 10 (100%)
## 
## Estimates assuming interval level:
## 
##              Omega (total): 0.86
##       Omega (hierarchical): 0.85
##    Revelle's omega (total): 0.89
## Greatest Lower Bound (GLB): 0.89
##              Coefficient H: 0.87
##           Cronbach's alpha: 0.86
## Confidence intervals:
##              Omega (total): [0.84, 0.89]
##           Cronbach's alpha: [0.84, 0.88]
## 
## Estimates assuming ordinal level:
## 
##      Ordinal Omega (total): 0.86
##  Ordinal Omega (hierarch.): 0.86
##   Ordinal Cronbach's alpha: 0.86
## Confidence intervals:
##      Ordinal Omega (total): [0.84, 0.89]
##   Ordinal Cronbach's alpha: [0.84, 0.88]
##